From local to global: Extrapolating experiments
The use of randomised control trials (RCTs) in evaluating the design and efficacy of policies has exploded in the last decade. New papers appear every week. But while RCTs are quickly becoming the gold standard for impact evaluations in international development and aid interventions, questions persist about what the results of an RCT in one context can tell us about the probable results of similar programme implemented in another context. Indeed, such questions are not unique to RCT’s but apply to the full set of empirical tools that economists apply in estimating policy impacts and outcomes.
Does context matter?
External Validity—the degree to which a study’s results can be generalized to other contexts— has so far been largely a matter of assumption or aspiration. Is the finding of a particular study primarily the result of factors that all humans generally share (like responses to incentives or behavioral biases) or local contextual factors (like attitudes toward women’s education or the state of the local labor market)? To make things even more complicated we can expect that in most cases both global and local characteristics play a role. That makes assessing external validity complex, but not hopeless. If we know what local factors affect outcomes, we can adjust for those from context to context to make better predictions (for instance, if we know that local labor market conditions matter we can adjust the predicted size of impact higher or lower based on the comparison).
With a sufficient number of consistent replications of an experiment, external validity becomes an empirical question: we can ask whether evidence from one or more experimental sites is able to predict impacts at other experimental sites. Some recent work (Alcott [2014], Pritchet and Sandefur [2013], Gechter [2015], and Vivalt [2015]) has used results from a handful of similar experiments to assess external validity (or in Vivalt’s case, a meta-analysis of an evidence base cutting across many domains). We took another approach to help illuminate how having a large experimental or non-experimental evidence base may help in predicting outcomes in additional contexts.
Since there are no RCTs that have more than a dozen replications to date, we built off a natural experiment paper (Angrist and Evans 1998) which used data from the US, but where data are now available for many more countries and multiple years: the effect of having the first two children born to a family being the same sex (“same-sex”, i.e., boy-boy or girl-girl) on the probability that a mother will have more than two children. If you want to see the technical details of our analysis, additional details are below. For those of you mostly interested in the take-aways, here’s a brief summary.
With a sufficient number of consistent replications of an experiment, external validity becomes an empirical question
Does ‘same-sex’ always increase the likelihood of having a 3rd child?
Angrist and Evans found that having two children of the same sex did indeed increase the likelihood of having a third child in the US, using data from 1980 and 1990. When we expanded the analysis to include all the data available (160 country-years spanning 60-plus countries and 50 years), we found generally similar results. But the effect sizes range from slightly negative to a 15% increase in likelihood of having a third child. Even with effectively 160 experiments, that makes it hard to make a policy-relevant prediction since the effect in another context could be either negative or positive.
Then we assessed whether adding additional adjustments for factors likely to affect incremental fertility (e.g. a mother’s education, GDP per capita, labor force participation of women, the total fertility rate, etc.) allowed us to make better predictions across the sample. Indeed, including more factors did decrease average prediction error to close to zero. We also looked at other approaches to increasing prediction accuracy, assessing whether the results in a country at a point in time accurately predicted results in the future, or whether the results from a region (within a country) or a country accurately predicted results in a neighbor.
More data: How much is enough?
The more data used to make a prediction, the better the prediction results, which isn’t surprising. What was surprising was that the results of a neighboring country in the same year were more predictive than results from the same country from an earlier time period. We also tested various other configurations of adjustments, for instance micro- and macro-data, looking for patterns in improving predictive accuracy. While in general we found that more data—in other words, more experimental results—led to better predictions, the results weren’t uniform. In some cases micro-level data worked better than macro-level data and in others, the reverse.
External validity is not a yes-no question
The bottom line is that while this example shows the possibility of using a group of natural experiments to increase our knowledge about the likely effects of similar programs in other contexts we still have a long way to go before we have a solid grasp on how to create accurate predictions—and that the process will likely be unique to different domains.
more data—in other words, more experimental results—led to better predictions
Understanding better how to extrapolate the results of labour market interventions may not tell us anything concrete about how to better extrapolate the results of other interventions, but we hope it is a useful first step.
Technical annex
Figure 1 below presents the country-year treatment effects of same-sex on incremental fertility (y-axis) plotted against the proportion of women who have completed secondary schooling (x-axis).
Figure 1: Effect of 'same sex' on probability of more children by proportion of women that complete secondary school
Source: Authors' calculations based on data from the Integrated Public Use Microdata Series-International (IPUMS-I).
Notes: The graph plots the size of the treatment effect of Same-Sex on having more children by the proportion of women with a completed secondary education based on data from 142 census samples. The graph also displays heterogeneity by geographic region.
Figure 1 is an illustration of how proving external validity remains a non-trivial challenge. Almost all of the treatment effects observed are greater than zero, which means that across each sample, having two children of the same sex does slightly increase a woman’s probability of having a third child. However, the size of this effect ranges from slightly negative to 0.15. The fact the range includes zero implies that in some cases, there may be no effect at all on a woman’s incremental fertility.
Context matters for external validity
The treatment effects above are positively correlated with country-year education, and similar relationships hold for other individual and country-level covariates (such as mother’s age, GDP per capita, the total fertility rate, and women’s labour force participation). This suggests that taking into account an experimental site’s characteristics should improve accuracy and quality of predicted estimates for target sites.
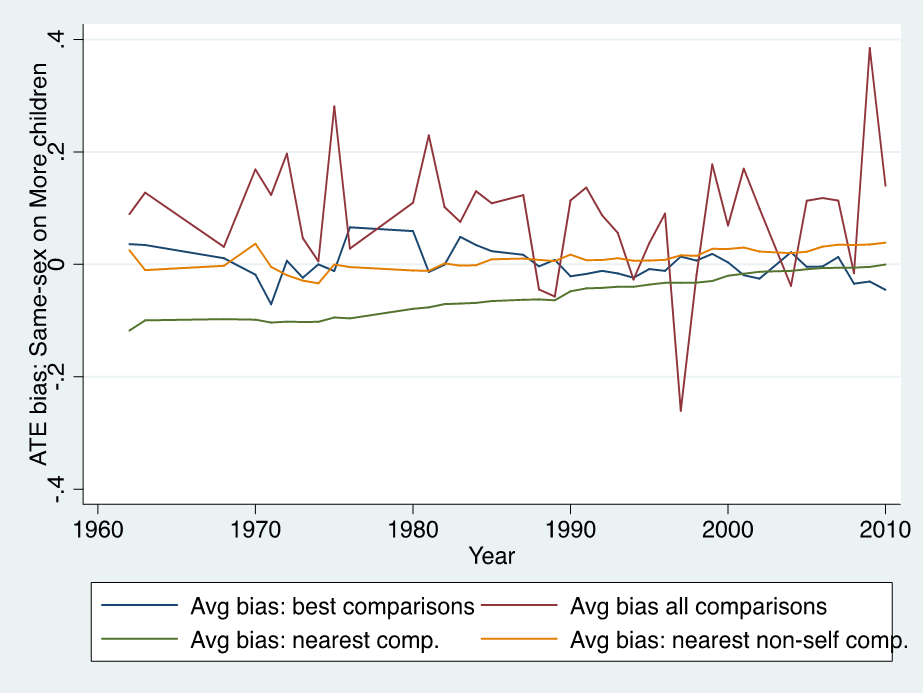
Figure 2: Extrapolation error model: Changes prediction error over time
Figure 2 depicts the average in-sample error, at each point in time, using variables such as GDP per capita, education, the total fertility rate, and labour force participation of women to predict variation in the treatment effect across all combinations of experiments. Strikingly we note that over time, both the prediction error (the blue line) and the degree of dispersion (error bands) approach zero. In other words, with sufficient data, the model is on average able to explain variation in treatment effects across sites accurately.
Figure 3: Out-of-sample extrapolation
Figure 3 examines a more challenging scenario: out-of-sample extrapolation, where we use four alternative models to extrapolate the treatment effect from experiments available at a point in time to experiments in the next period. When using the extrapolation error model depicted in Figure 2 to select the reference experiment most similar to the target site of interest, average extrapolation error is low and centered around zero (blue line). When a simple rule of thumb is used to select the reference site used to predict the treatment effect in the target (using nearest geographical location, either allowing for or excluding own-country comparisons), prediction error also converges to close to zero with sufficient data, but with fewer experiments is less reliable. In particular, somewhat surprisingly, using the nearest geographical comparison (allowing for own-country comparisons, green line) fares worse than using the nearest non-own country geographical comparison (yellow line), reflecting the extrapolation error associated with differences in calendar time between censuses within the same country. It is notable that when using all available experiments (red line), the prediction error does not converge to zero, even as the quantity of data accumulates over time.
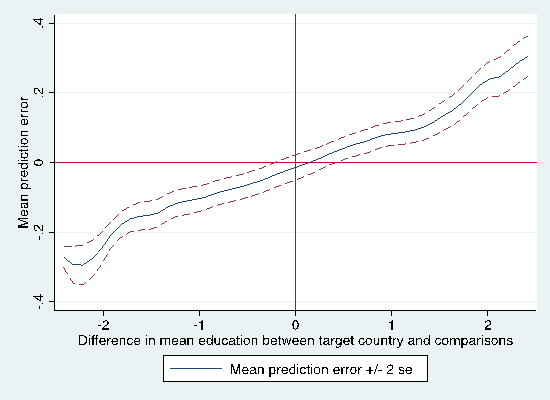
Figure 4: Effect of differences in education on extrapolation error
If, with sufficient data, it is possible – at least in this application – to predict treatment effects across experiments, what drives extrapolation error? Figure 4 shows how differences between reference and target site characteristics can affect prediction error. As expected, we see that when reference and target sites have similar levels of educational attainment, extrapolation error tends to be small. However, when education differs, even by one standard deviation, the approximate equivalent of one point on a four point illiteracy scale, the extrapolation error increases to around 0.05, roughly equal to the magnitude of the overall treatment effect.
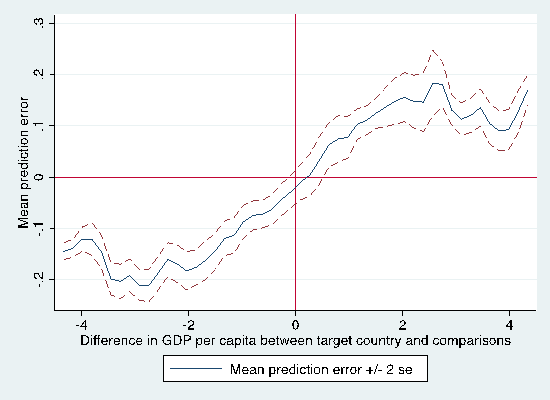
Figure 5: Effect of differences in GDP on extrapolation error
Figure 5 plots a similar relationship with differences in GDP per capita on the x-axis. Again, when reference and target sites have similar GDP per capita, extrapolation error tends to be low, while a one standard deviation ($9680) difference in GDP per capita is associated with extrapolation error of 0.05.
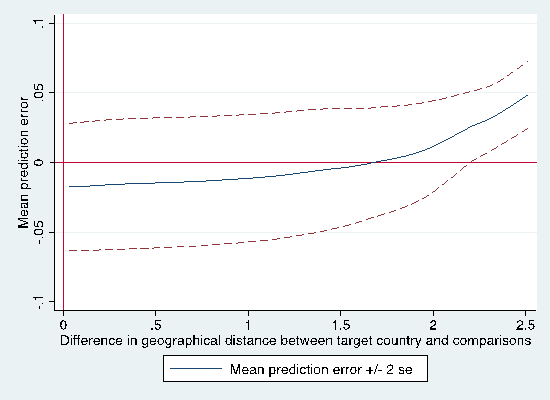
Figure 6: Effect of differences in geographic distance between target and reference sites on extrapolation error
Figure 6 plots the same relationship for within-region geographical distance (i.e., excluding country pairs separate by oceans). In contrast to figure 4 and 5, this graph shows a relatively flat relationship. This suggests that the main driver of extrapolation error may not be geographical distance per se, but differences in underlying economic factors.
Micro vs. Macro: Does using individual-level variables, or country-year variables reduce extrapolation error?
To explore this question, we repeated the exercise depicted Figure 3 using the following, varying the set of predictive variables: no covariates, only micro covariates, only country-year (macro) covariates, and all covariates.
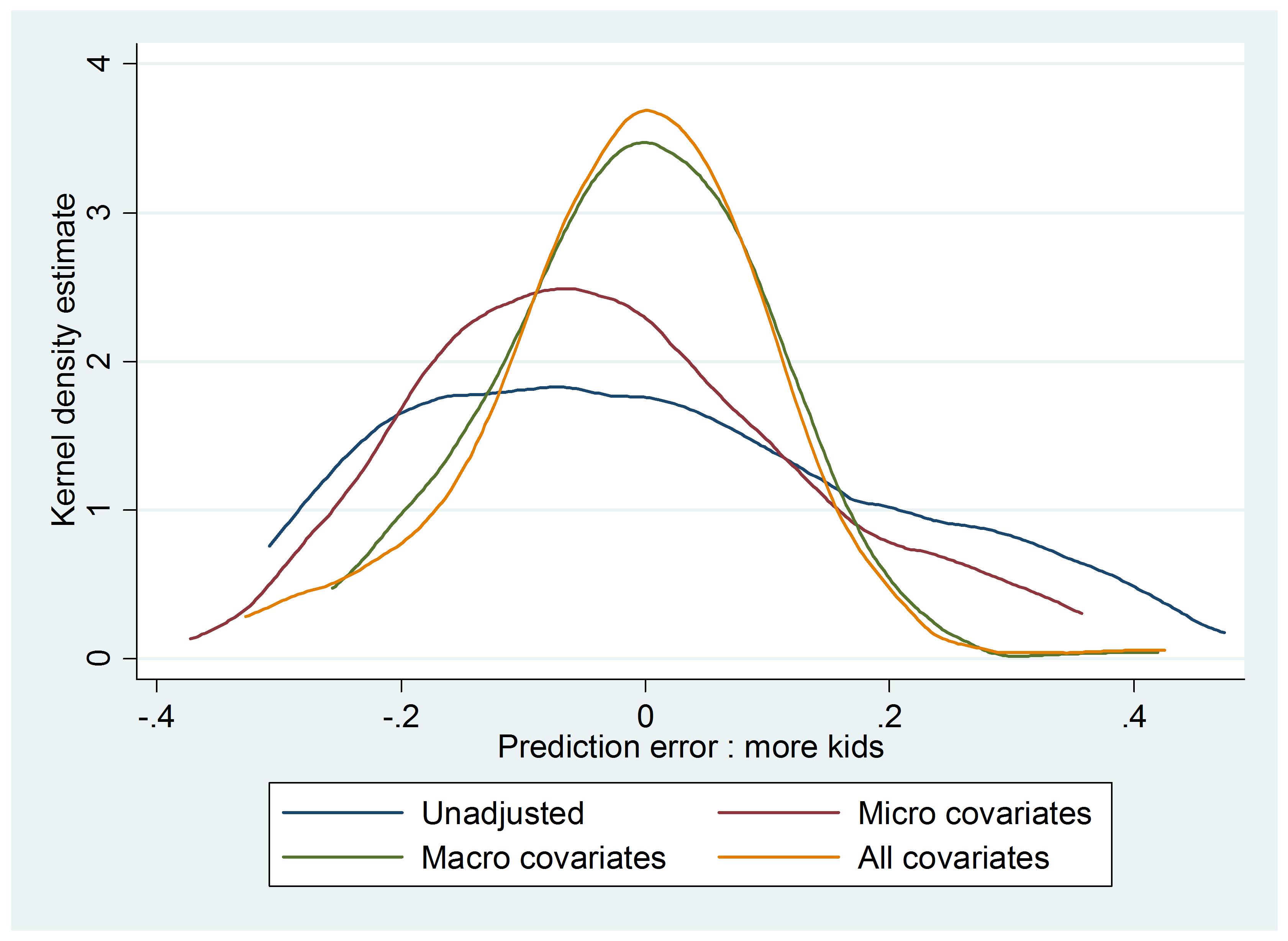
Figure 7: The effect of micro vs. macro covariates on extrapolation error for the effect of same sex on more kids
In Figure 7, we note that using either micro or macro covariates (red line and green line respectively) significantly improve upon a naïve extrapolation (blue line), with the full covariate set (yellow line) typically, but not uniformly, outperforming the alternatives. While this leads to the plausible conclusion that more covariates are always better to improve external validity, in Figure 8 we depict the same exercise but instead use another outcome, namely looking at the effect of same-sex on whether or not the mother is working. In this case, we note that micro covariates do not improve the external validity of predictions, whereas macro covariates do. At the same time, at least in this application, even a rudimentary set of macro covariates is useful in improving the external validity of predictions.
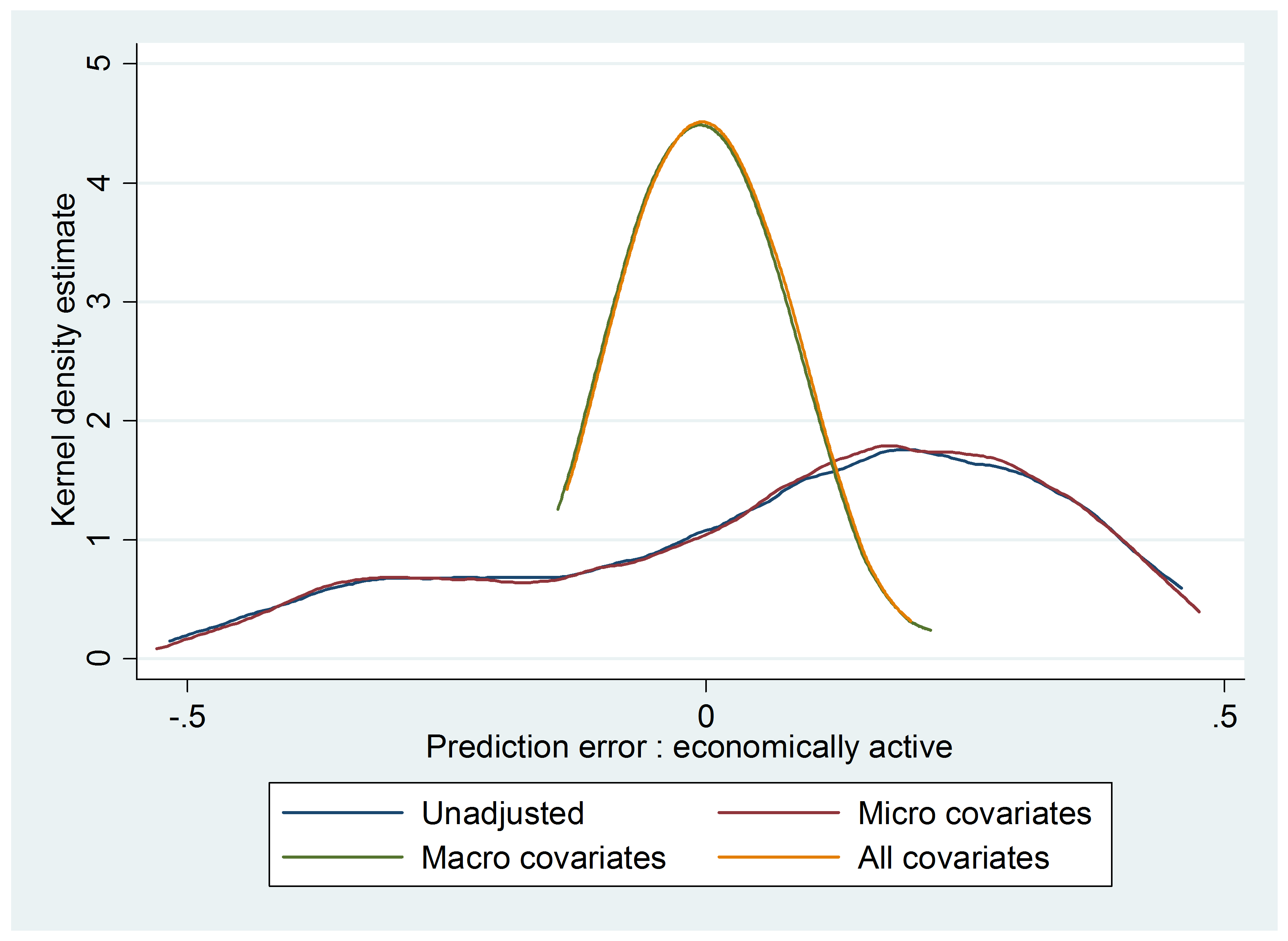
Figure 8: The effect of micro vs. macro covariates on extrapolation error for the effect of same sex on mother working
Qualifications and conclusions
Is external validity possible in experiments? Yes, but with three significant qualifications. First, there must be sufficient good evidence. Second, the reference experimental evidence base must be appropriately screened for comparability on the basis of reliable covariate information. Third, and most important, like any possible result, the results presented here are circumscribed by the particulars of the case study and data; each application and experimental evidence base will face its own challenges of external validity. Nonetheless, each context and application within which we can empirically test and characterise the extent of external validity adds value and improves future processes for applying empirical results in new contexts.
References
Angrist, Joshua, and William Evans (1998), Children and Their Parents’ Labor Supply: Evidence from Exogenous Variation in Family Size,” American Economic Review, Volume 88, Number 3, pp. 450-477.
Allcott, Hunt (2014), “Site Selection Bias in Program Evaluation,” manuscript, New York University.
Campbell, Donald T. (1957), “Factors Relevant to the Validity od Experiments in Social Settings,” Psychological Review, Volume 54, Number 4, pp. 297-312.
Lalonde, Robert (1986), “Evaluating the Economic Evaluations of Training Programs with Experimental Data,” American Economic Review, Volume 74, Number 4, pp. 604-620.
Pritchett, Lant, and Justin Sandefur (2013), “Context Matters for Size: Why External Validity Claims and Development Practice Don’t Mix,” Center for Global Development Working Paper 336.
Gechter, Michael (2015), “Generalizing the Results from Social Experiments: Theory and Evidence from Mexico and India,” Manuscript.
Vivalt, Eva (2015), “How Much Can We Generalize from Impact Evaluation Results?”, manuscript, New York University.